EVOLUTION DE LA GEODESIE
A. La géodésie est la science qui détermine la forme
et les
dimensions de la Terre dans l'espace à trois dimensions.
A partir des Grecs et jusqu'à la fin
du XVII° siècle, il est admis que la terre est sphérique. La réponse
à la question de sa forme est donc simple, la seule inconnue réside
en la longueur du rayon terrestre. La détermination de cette grandeur
se pose alors comme l'activité propre des savants géodésiens.
Une seule technique dite "méthode
des arcs", est employée ; elle fut élaborée dans son principe
par Eratosthène au III° siècle av. J. C., et met en oeuvre des mesures
de distances à la surface de la terre et des mesures astronomiques,
c'est-à-dire des mesures de directions de la verticale. On trouvera
cette méthode exposée à la BNF dans la partie « Dossiers pédagogiques »
du site « mesurer la Terre »:
http://www.bnf.fr/web-bnf/expos/ciel/maths/pdf/mesurt2.pdf
Ou bien sur le site de Serge Mehl:
http://chronomath.irem.univ-mrs.fr/chronomath/Eratosthene.html
« En astronomie, il se distingua
par son remarquable calcul de la longueur du méridien terrestre qu'il
évalue à environ 40000 km en remarquant qu'au solstice d'été, le soleil
est au zénith à Assouan (Syène à l'époque) au sud et approximativement
(à 3° près) sur le même méridien qu' Alexandrie où, au même moment,
l'ombre d'un obélisque montre que les rayons solaires sont inclinés
de 7°12' par rapport à la verticale. Si A désigne Alexandrie, dire
que le Soleil est au zénith signifie que l'angle x est nul.
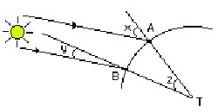
D'une façon générale : si A et B sont
deux lieux situés sur un même méridien (même longitude), notons x
et y les mesures en radians des angles entre les rayons du soleil
(supposés parallèles) et les verticales en A et B, z la mesure en
radians de l'angle ^ATB, R le rayon de la Terre (supposée sphérique),
L sa circonférence et d la mesure de l'arc AB. On a alors :
z = | x - y
| , R = d/z , L = 2pR
Si on utilise les degrés, on aura L
= 360d/z.
Dans le cas qui nous intéresse, d =
830 km (5000 stades, distance connue car parcourue à pied par les
armées...) et 7° 12' = 7,2°. On a alors L = 41500 km.
Si l'on considère le rayon de la Terre
à l'équateur : 6378 km, on obtient aujourd'hui 40074 km. Le résultat
d'Eratosthène est donc tout à fait remarquable : 3% d'erreur. »
En fait cette définition de la géodésie
par son "objet" seul : la . forme de la terre, méconnaît
une réalité essentielle de toute science : ses implications sociales,
politiques et religieuses. Dès l'origine la géodésie a comporté des
aspects autre que celui de la détermination d'une surface dont la
connaissance pure n'était l'objectif que de quelques savants. Concrètement
la surface terrestre n'est pas une sphère mais revêt une forme extrêmement
complexe donnée par la nature ou modifiée par l'homme. La connaissance
de cette surface là, de ses détails, non dans leur nature mais dans
leur position et leurs grandeurs implique des aspects très nombreux
de la vie des hommes, politiques, religieux, sociaux : lever
l'impôt ou faire la guerre, penser le Monde pour les Eglises les voyageurs,
marchands. Rappelons la mise à l’index des idées de Copernic en 1616
par l’Eglise catholique. Ces aspects affectent profondément le développement
de la géodésie et de la cartographie. A cet égard l’exposition de
la BNF « Ciel et Terre » est particulièrement démonstrative.
http://www.bnf.fr/web-bnf/expos/ciel/index.htm
La géodésie peut donc être caractérisée
comme l'unité de deux objectifs : connaissance globale de la forme
de la surface terrestre et connaissance concrète des particularités
de la surface réelle.
La synthèse, jusqu'à une époque très
récente (milieu du XX° siècle) a pris la forme de la détermination
des coordonnées géométriques d'un certain nombre de points dits « points
géodésiques » considérés comme appartenant à une surface mathématiquement
parfaite, la sphère d'abord, l'ellipsoïde ensuite. La détermination
de la localisation de chaque élément particulier de la surface, à
partir des points géodésiques étant assurée par une technique particulière
: la topographie et la représentation de ces éléments sur une surface
plane par la cartographie.
Ainsi depuis l'antiquité grecque jusqu'au
milieu du XX° siècle, la géodésie a-t-elle eu pour tâche de déterminer
une surface mathématique simple et de localiser des points sur cette
surface. Cette géodésie peut être dite avec le recul : bidimensionnelle
et géométrique.
B. La problématique de la sphère, solide et immobile.
( XVI'siècle)
La surface de référence est donc supposée
sphérique. En ce qui concerne la localisation des points, le problème
est double :
·
d'une part déterminer la position relative
de ces points.
·
d'autre part assurer leur localisation absolue
sur la sphère, modèle théorique. Ce dernier problème imposant de définir
un référentiel fixe par rapport à la sphère :
Dans cette première problématique profondément
marquée par l'astronomie, le référentiel s'impose de lui-même : il
a pour élément le centre de la sphère, l'axe de rotation de la sphère
céleste censée tourner autour d'une terre immobile, (ceci impose l'équateur)
et un grand cercle polaire arbitrairement choisi. Tout point est localisé
sur la surface par deux coordonnées, deux angles; latitude et longitude.
Les mesures astronomiques de hauteur d'astres permettent d'obtenir
la latitude de différents lieux. En revanche l'absence de « garde
temps » empêche toute détermination astronomique de longitude.
Celles-ci ne peuvent être obtenues que par des mesures relatives de
position sur la surface terrestre. Ces mesures sont alors essentiellement
des distances obtenues à partir des temps de parcours pédestres ou
maritimes.
C. L'ellipsoïde, fluide et en mouvement : XVIII° et
XIX° siècle.
Entre 1543 « De
revolutionibus orbium cælestium libri », Copernic
et 1687 « Philosophiae naturalis
principia mathematica », Newton, un certain nombre de découvertes révolutionnent
la conception de la géodésie.
-
la terre est en mouvement, sur elle même et autour
du soleil
-
ce mouvement impose une forme ellipsoïdale.
Les grands problèmes de la géodésie
deviennent donc
-
la détermination de l'ellipsoïde : grand axe et aplatissement
-
la localisation de points sur cet ellipsoïde.
En ce qui concerne la première question,
la « méthode des arcs » reste la technique la plus appropriée.
Selon qu'elle est utilisée à l'équateur ou au pôle elle permet de
déterminer grand axe et petit axe, donc l'aplatissement. Cette méthode
se trouve nettement améliorée par la qualité des mesures:
-
la différence de latitude est obtenue à partir de
mesures astronomiques utilisant la lunette.
-
la distance est mesurée par la technique de triangulation
La localisation des points.
Le référentiel : il reste unique et
déterminé par les phénomènes astronomiques : l'ellipsoïde est
de révolution et en rotation autour de son axe ; ce dernier sera donc
choisi comme élément du référentiel avec du même coup l'équateur.
Un plan méridien choisi comme origine des longitudes vient compléter
ce système dans lequel tout point est, comme dans la première problématique
déterminé par ses deux coordonnées géographiques, longitude et latitude.
Mais cette nouvelle problématique va
rapidement se complexifier. Mac-Laurin et Clairaut (milieu du XVIII°)
posent la terre comme figure d'équilibre d’une masse fluide pesante
en rotation. I1 devient possible de déduire de mesures de la pesanteur
une valeur de l'aplatissement meilleure que celle déduite de la méthode
des arcs.
I1 reste acquis, pour l'époque que la
terre est ellipsoïdale et en mouvement, et cette ellipsoïde peut être
déterminé de deux façons :
-
à partir de mesures géométriques d'angles et de distances
entre points de la surface topographique , mesures auxquelles on fait
subir des corrections pour tenir compte du relief.
-
à partir de mesures "dynamiques" du champ
de la pesanteur (attraction universelle et forces de rotation). La
Terre, la surface terrestre est alors définie comme surface équipotentielle
du champ de la pesanteur.
La géodésie se scinde à ce moment en
une :géodésie géométrique et une géodésie dynamique. Pendant longtemps
la première va rester principale car c'est elle qui résout le problème
concret de la localisation. Cependant c’est dès cette époque, la seconde
qui assure la détermination la plus précise de l'aplatissement. Ces
deux géodésies peuvent être qualifiées de « bidimensionnelle »
Elles ont toutes deux comme objet fondamental une surface de référence
supposée ellipsoïdale.
D. Le géoïde.
A peine les résultats de Clairaut sont-ils
reconnus que les faits viennent les relativiser. Pas plus que la surface
topographique, la surface équipotentielle du champ de la pesanteur
ne saurait être un ellipsoïde puisque les masses montagneuses « aléatoires »
vont exercer une attraction aléatoire déformant l'ellipsoïde idéal.
La géodésie dynamique est peu à peu amenée à reconnaître que la surface
qu'elle cherche à déterminer n'est qu'approximativement un ellipsoïde.
Elle attribue un nom à une surface équipotentielle particulière, celle
correspondant, dans les secteurs océaniques, au « niveau moyen
des mers ». Cette surface est, dans les secteurs continentaux,
supposée être le « prolongement » du niveau moyen des mers
: son nom est le géoïde. Remarquons qu'il ne diffère au plus que d’une
centaine de mètres d'un ellipsoïde alors que l'écart entre la surface
topographique et l’ellipsoïde peut atteindre 8 km.
Les référentiels.
La notion d'un référentiel unique disparaît
avec celle d'une surface mathématique simple déterminée, comme surface
de la terre. D'autre part en effet la géodésie dynamique précise son
propre référentiel
-
centre 0 voisin du centre de gravité des masses terrestres
-
axe Z parallèle à l'axe moyen de rotation.
-
axe OX tel que le plan OXZ contienne un point de
l'observatoire de Greenwich
I1 est donc indépendant de toute référence
à un ellipsoïde. D'autre part la géodésie géométrique multiplie ses
propres référentiels en multipliant ses ellipsoïdes et leur position
par rapport à la surface topographique (ces deux ensembles constituent
un « datum »). En effet, comme il n'existe pas un seul ellipsoïde,
surface géométrique mathématiquement simple de la Terre , divers géodésiens
peuvent définir ce qui leur semble être le "bon ellipsoïde",
et qui n’est en fait que l'ellipsoïde le plus approprié à leur objectif
particulier : la représentation du secteur de la surface topographique
qu'ils doivent localement, à l'échelle de leurs pays, représenter.
E. La géodésie tridimensionnelle.
Avant même le lancement des premiers
satellites artificiels un certain nombre de géodésiens étaient préoccupés
par les difficultés que rencontre la géodésie classique dans certaines
de ses définitions ou de ses conclusions.
-
convient-il de représenter la surface topographique
sur l'ellipsoïde ou sur le géoïde, et dans ce cas comment en faire
la représentation plane ?
-
comment peut-on définir l'image ellipsoïdale d'un
point de la surface topographique. Faut-il considérer sa projection
orthogonale sur l'ellipsoïde ou ne vaut-il pas mieux adopter la définition
de transfert suivant la ligne de force de la pesanteur ?
-
comment peut-on réduire à l'ellipsoïde les observations
angulaires effectuées selon la verticale physique ? etc.
En 1956 au cours d'un symposium réuni
à Münich que le géodésien anglais Hotine, présente un aspect géodésique
nouveau qui devient très rapidement la géodésie tridimensionnelle.
I1 semble que Molodensky avait également vers 1948 émis un certain
nombre de conclusions analogues mais qui n'avaient été diffusées qu'en
U.R.S.S.
Pour Hotine le problème de la géodésie
doit être repensé, non dans l'espace à deux dimensions de la surface
de l'ellipsoïde de référence, dimensions auxquelles on en ajoute une
troisième tout à fait indépendante l'altitude, mais dans le cadre
d'un système à trois dimensions défini par un trièdre trirectangulaire
de coordonnées, et par un certain nombre de trièdres auxiliaires locaux,
rattachés à ce dernier.
Les paramètres qui définissent la
géodésie en un point de la surface topographique sont ses coordonnées
spatiales (X,Y,Z) et les cosinus directeurs de la verticale en ce
point.
Le but de la géodésie devient la description
spatiale directe de la forme de la surface topographique, sans chercher
à lui imposer a priori le support approché de l'ellipsoïde. A la description
géométrique doit s'ajouter la description dynamique, en particulier,
en chaque point on se proposera de connaître le potentiel et la pesanteur
et on fera concourir tout l'ensemble à une synthèse générale. C'est
un très beau programme, c'est celui que la géodésie s'est toujours
proposé, mais conçu sous un aspect plus synthétique, sans séparer
a priori les variables et sans s'imposer le carcan de l'ellipsoïde
� ce qui ne veut d'ailleurs pas dire que l'on n'utilisera pas ce dernier
à titre d'auxiliaire commode, pour linéariser certains problèmes dont
la solution n'est pas du premier degré.
Les mesures sur lesquelles se base la
géodésie tridimensionnelle sont
-
les mesures angulaires azimutales habituelles ;
-
les mesures de distances zénithales,
-
les mesures de pesanteur qui concourent simultanément
avec les mesures de nivellement à définir la pesanteur et le potentiel,
-
les mesures astronomiques de latitude longitude et
azimut.
I1 n'y a là rien de bien nouveau sinon
l'emploi conjugué de l'ensemble de ces moyens et la manière de leur
utiliser. La géodésie tridimensionnelle ne s'occupe que de décrire
ce qui est visible et directement accessible à l'expérience, elle
cherche à définir un polyèdre géodésique ou plus exactement un ensemble
de points dont les coordonnées trirectangulaires ainsi que les autres
éléments : direction de la verticale, intensité de la pesanteur, potentiel
soient déterminés, et elle oriente ses calculs de manière à l'obtenir.
Ajoutons à cela que les méthodes tridimensionnelles se sont trouvées
fort bien adaptées à l'exploitation des travaux sur satellites.
Ainsi la géodésie est-elle libérée de
tout a priori. Elle admet la complexité de son objet, elle reconnaît
qu'aucune loi simple ne pourra le représenter. Son « résultat »
ne peut plus être qu'une masse énorme d'informations que recueille
le satellite et traite l'ordinateur. Au sein de cette complexité,
les lois, les invariants ne se présentent plus que comme des moyens
d'économiser de l'information. L'information, c'est-à-dire la représentation
du particulier a détrôné la « loi »et règne en maître. Comme
la société, la géodésie s'informatise.
Les nombreux sites internationaux sur
ce thème montrent comment on calcule le géoïde, la variation du niveau
des mers, l’altimétrie des océans et des lacs voir par exemple le
texte à l’url : http://www.omp.obs-mip.fr/omp/gos/geodesie.html
|
